1. Pourquoi trier ? >> vers le sommaire
Lorsqu'une relation d'ordre a été établie, par exemple dans un tableau, les opérations sont très rapides. Le minimum est le premier élément du tableau, le maximum le dernier élément... On a donc un accès temps constant pour les trouver après. Par ailleurs, pour trouver un élément quelconque, l'algorithme dichotomique que nous verrons par la suite est parfait sur un ensemble trié. Dans certains cas, il est parfois aussi rapide (sinon plus) de trier une série pour en faire ressortir le maximum et le minimum, que de le chercher de façon brutale !
On a aussi des tris qui constituent directement une finalité : l'annuaire (ville puis alphabétique), l'agenda (mois puis jour), le Z-sorting (trier les objets en 3d selon leur éloignement, pour les jeux vidéos pour exemple). Il s'agit donc d'une connaissance tout à fait fondamentale !
2. Les caractéristiques du tri >> vers le sommaire
Il existe de très nombreux tris. Il faut donc expliciter
leurs caractéristiques ; commençons par la mémoire :
- Si le tri est interne, les données à trier sont contenues
sur la mémoire principale. Les opérations coûteuses qui
vont établir la complexité sont les calculs et comparaisons
effectués.
- Si le tri est externe, les données à trier ne sont pas contenues
sur la mémoire principale. Les opérations coûteuses sont
alors les temps d'accès à la mémoire qui contient les
données.
Dans notre cas, on s'intéressera à des tris internes.
La façon dont on stocke les données n'est pas notre problème.
Notre préoccupation portera donc uniquement sur les caractéristiques
suivantes :
- Tri stable. Si les clés sont identiques, l'algorithme n'en modifie
pas l'ordre.
- Tri sur place. La mémoire supplémentaire dont on a besoin
pour effectuer le tri est négligeable.
3. La borne du tri par comparaison >> vers le sommaire
Il existe plusieurs familles de tri. L'une d'elle compare les
éléments pour les trier ; c'est donc logiquement que nous l'appelons
la famille du "tri par comparaison". Il existe de nombreux moyens
de trier en comparant :
- Insertion. On considère chaque élément et on les insère
à la bonne position par rapport à ceux déjà triés.
- Echange. Si deux éléments ne sont pas dans dans leurs bonnes
positions, on les échange (permutation).
- Sélection. On repère un élément caractéristique
(le maximum, le minimum...) et on l'insère en premier. On recommence
l'opération sur les éléments restants.
- Enumération. On compare l'élément avec tous les autres,
sa position étant donné par le nombre d'éléments
qui lui sont supérieurs (ou inférieurs).
- Autre. Enfin, on a des algorithmes qui ne relèvent d'aucune de ces
catégories. Ils sont en général spécialisés.
Comme nous avons de nombreuses familles de tri par comparaisons, donc de
nombreux algorithmes, il est utile de savoir dans le meilleur des cas la complexité
à laquelle on peut parvenir. Pour cela, on représente les comparaisons
à effectuer entre les éléments sous forme d'un arbre
; par exemple, pour 3 éléments :
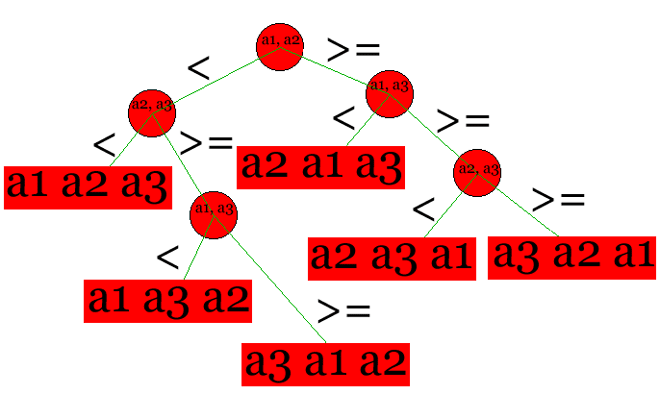
Cet arbre est nommé arbre "de décision". Les feuilles
représentent les permutations devant être effectuées pour
que le tableau soit trié. On peut donc faire une démonstration
classique :
4. L'algorithme de tri le plus simple : le tri à bulles (bubble sort) >> vers le sommaire
Le principe du tri à bulles est, qu'au fur et à mesure de l'éxécution, les valeurs importantes vont remonter tandis que les valeurs faibles vont descendre. Ceci illustre l'idée d'une bulle dans un liquide : plus un volume est important, moins la bulle est dense, et donc plus elle remonte dans le liquide.
Une manière simple de mettre en oeuvre ceci est :
soit T un tableau de taille N
pour(entier i = 0;i<N;i++){
pour(entier j = 0;j<N-1;j++){
si(T[j]>T[j+1]){
// On va échanger T[j] et T[j+1] : permutation
element
tmp = T[j]
T[j]
= T[j+1]
T[j+1]=tmp
}
}
}
T est maintenant trié dans l'ordre croissant
Un exemple pour comprendre le fonctionnement :
Bien évidemment, vous pouvez trier n'importe quoi, le
tout étant d'avoir implémenté une relation d'ordre entre
les éléments (l'interface Comparable). Ainsi, si on veut trier
des lettres :
Le principe pour faire le tri suivant ce principe est simple : si un élément est inférieur au suivant, on l'inverse. On passe au suivant. Lorsqu'on a finit, on repart du début. On s'arrête lorsque c'est trié.
Le problème est que, si un humain voit que la liste est
triée, il n'en est pas de même d'un ordinateur ! En effet, avec
notre algorithme, si la liste est déjà triée, il va malgrè
tout faire ses opérations dessus... Imaginons qu'on lui fournisse une
liste triée de 10 éléments, il va faire 100 tests inutiles.
C'est loin d'être optimisé... Ainsi, on propose une autre implémentation
du tri à bulle qui permet de s'arrêter lorsqu'on a trié
:
soit T un tableau de taille N
soit trie un booleen
tant que(trie=vrai){
trie = faux
pour(entier i=0;i<N-1;i++){
si(T[i]>T[i+1]){
// On va permuter comme avant
element
tmp = T[i]
T[i]
= T[i+1]
T[i+1]
= tmp
trie=vrai
}
}
}
T est maintenant trié dans l'ordre croissant
Le principe est simple : on comment par dire que nous n'avons pas trié. On va parcourir toute la liste : dès qu'on fait un tri, on le signale. Si aucun tri n'a été fait, c'est donc que l'ensemble était déjà ordonné et on peut s'arrêter.
Dans la première implémentation, le tri était
en 
(n²) : dans tous les
cas, il fallait faire les deux boucles. Dans la seconde implémentation,
plus maligne, on a deux cas :
- Soit l'ensemble est déjà trié (meilleur des cas). On
va alors le parcourir intégralement pour s'apercevoir que c'est le
cas : O(n)
- Soit il est trié en ordre inverse (pire des cas). Notre algorithme
va alors être équivalent à une double boucle, d'où
une complexité en O(n²) ; pour rappel, cette complexité
est très mauvaise par rapport au n.log(n)...
Comme on le voit, ce tri est fait sur place (pas besoin de créer un nouveau tableau). De plus, il est stable. Cependant, ce sont ses seuls avantages, puisqu'il a une très mauvaise complexité...
5. Tri par sélection (selection sort) >> vers le sommaire
On cherche le plus petit élément et on le place
en premier place. On cherche le deuxième plus petit élément
et on le place en deuxième place, etc. Pour résumer, on sélectionne
la valeur qui occupe cette case quoiqu'il en soit, on la met là, et
on cherche la valeur qui doit occuper la case suivante. Regardons le code
:
soit T un tableau de taille N
pour(entier i=0 ; i<N-1;i++){
entier minimum = i
pour(entier j=i+1;j<N;j++){ //
on va chercher le minimum
si(T[j]
< T[min) //a-t-on plus petit ?
min
= j // si oui, c'est le nouveau minimum
}
if(min!=i){ //si on a trouvé
un nouveau minimum
element
tmp = T[i] // alors on fait l'échange
T[i]
= T[i+1]
T[i+1]
= tmp
} // on peut aussi faire systématiquement
l'échange et se passer du test...
}
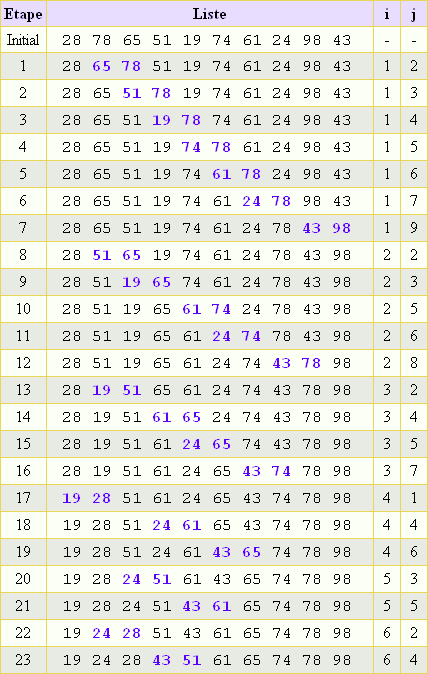
Exemple d'éxécution sur 28 78 65 51 19 74 61 24:
- On déclare que le minimum est 28. On regarde si on trouve un autre
minimum. Oui, c'est 19.
-> On permutte et on se retrouve avec 19 78 65 51 28 74 61 24
- On déclare que le minimum est 78. On regarde si on trouve un autre
minimum. Oui, c'est 24.
-> On permutte et on se retrouve avec 19 24 65 51 28 74 61 78
- On déclare que le minimum est 65. On regarde si on trouve un autre
minimum. Oui, c'est 28
-> On permutte et on se retrouve avec 19 24 28 51 65 74 61 78
- On déclare que le minimum est 51. On regarde si on trouve un autre
minimum. Non.
- On déclare que le minimum est 65. On regarde si on trouve un autre
minimum. Oui, c'est 61.
-> On permutte et on se retrouve avec 19 24 28 51 61 74 65 78
- On déclare que le minimum est 74. On regarde si on trouve un autre
minimum. Oui, c'est 65.
-> On permutte et on se retrouve avec 19 24 28 51 61 65 74 78
- On déclare que le minimum est 74. On regarde si on trouve un autre
minimm. Non.
Ou un exemple moins commenté :
Ce tri est en (n²)
: on parcourt le tableau du début à (presque) la fin, et à
chaque fois le sous-tableau correspondant. Dans le meilleur des cas, si le
tableau est déjà trié on gagnera un peu sur l'échange...
Sachant que dans le pire des cas, la théorie nous parle de n.log(n),
on peut en déduire que cet algorithme en n² n'est pas bon.
Comme pour le tri précédent, il est sur place (pas besoin de
consommer d'autres ressources) et stable.
6. Tri par insertion (insertion sort) >> vers le sommaire
On utilise souvent le principe d'un joueur de carte pour décrire
ce tri. On a un ensemble de cartes et on veut les trier : on insère
chaque carte à la bonne position parmis les cartes triées. L'algorithme
est le suivant :
soit T un tableau de taille N
pour(entier i=1 ; i<N;i++){
element cle = T[i] // l'élément
courant qu'on conserve
entier j=i-1
tant que(j>=0 et T[j]>cle){
T[j+1]
= T[j] // on fait un décalage
j--
}
T[j+1]=cle // et on l'insère
}
Exemple d'éxécution sur 28 78 65 51 19 74 61 :
- Initialisation : i vaut 1. cle vaut 78. j vaut 0. T[0]=28 est inférieur
à 78, on passe. T[j+1]=T[1]=78.
- i vaut 2. cle vaut 65. j vaut 1. T[1]=78 > 65. T[2] = T[1]. j vaut 0.
T[0]=28<65. T[1]=65.
-> on se retrouve avec 28 65 78 51 19 74 61
- i vaut 3. cle vaut 51. j vaut 2. T[2] = 78 > 51. T[3] = T[2]. j vaut
1. T[1] = 65 > 51. T[2] = T[1]. j vaut 0. T[0] = 28 < 51. T[1] = 51.
-> on se retrouve avec 28 51 65 78 19 74 61
- i vaut 4. cle vaut 19. j vaut 3. T[3] = 78 > 19. T[4] = T[3]. j vaut
2. T[2] = 65 > 19. T[3] = T[2]. j vaut 1. T[1] = 51 > 19. T[2] = T[1].
j vaut 0. T[0] = 28 > 19. T[1] = T[0]. j vaut -1. T[0] = cle.
-> on se retrouve avec 19 28 51 65 78 74 61
- i vaut 5. cle vaut 74. j vaut 4. T[4] = 78 > 74. T[5] = T[4]. j vaut
3. T[3] = 65 < 74. T[4] = cle.
-> on se retrouve avec 19 28 51 65 74 78 61
- i vaut 6. cle vaut 61. j vaut 5. T[5] = 78 > 61. T[6] = T[5]. j vaut
4. T[4] = 74 > 61. T[5] = T[4]. j vaut 3. T[3] = 65 > 61. T[4] = T[3].
j vaut 2. T[2] = 51 < 61. T[3] = cle.
-> on se retrouve avec 19 28 51 61 65 74 78
Récapitulons :
Le principe est simple : on part du 2ème élément. On le met là où il devrait être et on décale les autres. On prend le 3ème élément, on le met là où il devrait être et on décale les autres. On prend le 4ème, etc. etc.
Dans le meilleur des cas, le tableau est déjà trié.
On ne fait donc pas la boucle tant que : on se contente de parcourir tout
le tableau en faisant cle = T[i], j = i -1, T[j+1] = cle, ce qui est constant.
Donc, dans le meilleur des cas nous sommes en (n).
Dans le pire des cas, le tableau est trié à l'envers, on fait chaque boucle de façon complète. Comme nous l'avons vu, ce système de boucle imbriqué est en O(n²) : la première boucle se fait (n-1) fois et à chaque passage on fait un décalage.
Ce tri est fait sur place comme les précédents, et il est également stable.
7. Méthode "diviser pour régner" (divide and conquer) >> vers le sommaire
Par rapport à la borne théorique, les algorithmes
que nous avons vu ne sont pas très performants. On va alors faire appel
à une autre méthode pour résoudre le problème
: diviser pour régner. La stratégie est en 3 parties :
- Diviser. On coupe l'ensemble à traiter en plusieurs sous-ensembles
disjoints.
- Régner. On applique l'algorithme de manière récursive
sur chacun des sous-ensembles.
- Réunir. On fusionne les solutions des sous-ensembles pour obtenir
la solution finale.
C'est un peu le même principe que ce que nous avons vu dans les premiers algorithmes récursifs ou les arbres : le problème est trop compliqué, on le coupe alors jusqu'à se ramener à un cas simple. On sait traiter le cas simple, donc on fait remonter les résultats et on résout ainsi l'ensemble.
8. Tri par fusion (merge sort) >> vers le sommaire
Cet algorithme de tri utilise le principe précédent
: le problème du tri de plusieurs éléments est trop compliqué,
on va diviser l'ensemble à traiter en un cas simple. Quel est le cas
simple ? Un ensemble d'un seul élément ! Donc :
- On divise le tableau de données en sous-tableaux de taille n/2. Pour
diviser le tableau, c'est finalement une approche simple : on change les indices.
Ainsi, pour diviser un tableau de N éléments en 2, on considère
juste la partie qui va de 0 à (N/2)-1 et la partie de N/2 à
N.
- On applique de façon récursive le tri-fusion sur chacun des
tableaux au final.
- On fusionne des tableaux triés (i.e. en commancant par des tableaux
d'un élément) en les parcourant en parallèle et en mettant
la plus petite clé rencontrée dans un tableau résultat.
Le problème de ceci est la création de tableaux temporaires
!
Comme nombre d'algorithmes récursifs, son écriture
est assez simple :
méthode Tri-Fusion(T un tableau, p et r des indices){
si p<r {
entier q = (p+r)/2 // p et r sont
les indices du tableau : (p+r)/2 coupe en 2
Tri-Fusion(T,p,q) // on applique
l'algorithme sur la première moitié
Tri-Fusion(T,q+1,r) // on applique
l'algorithme sur la seconde moitié
Fusionner(T,p,q,r) // on rassemble
les résultats
}
}
Couper le tableau en 2 jusqu'à avoir des tableaux d'un élément
est donc relativement simple. La méthode importante de cette algorithme
est celle qui permet de Fusionner.
Lorsqu'on fait appel à la méthode Fusionner, on lui transmet
:
- Le tableau de données
- L'indice p, début du premier sous-tableau à fusionner
- L'indice q, fin du premier sous-tableau à fusionner. Implicitement
: q+1, début du second sous-tableau.
- L'indice r, fin du second sous-tableau à fusionner.
La taille résultat de la fusion est donc r-p+1 : la fin est r, le
début est p, et il y a une case de place car le second-sous-tableau
commence à q+1. Deux petits exemples pour s'en convaincre :
On va donc créer un tableau ayant le résultat de la fusion.
Dans ce tableau, on va mettre les éléments triés issus
des deux sous-tableaux. Pour cela, le principe est simple : on les parcours
en parallèle et on prend le plus petit élément de chacun
des sous-tableaux (rappel : ils sont triés !). Si un tableau ne contient
plus d'éléments, il suffira de prendre ce qui reste dans l'autre
tableau. Ainsi :
méthode Fusionner(T un tableau, p, q et r des indices){
Tableau tmp = tableau d'éléments de taille r-p+1
entier a=p, b=q+1 // on va modifier les indices en parcourant, on les met
de côté
pour(entier i=0;i<taille de tmp; i++}{
si(b>r || (a<=q &&
T[a]<T[b]){ // s'il n'y a plus d'éléments dans [q+1, r]...
//
ou si les éléments de [p, q] sont plus petits que ceux de [q+1,
r]...
tmp[i]
= T[a] // alors on prend un élément de [p, q]
a++
// et on avance l'indice dans le tableau [p, q]
}
sinon{ // si le plus petit n'est
pas dans [q+1, r] alors il est dans [p, q]
tmp[i]
= T[b]
b++
}
} // a cet endroit, tmp contient le tableau fusionné. Il va falloir
le recopier
pour(entier k=0;k<taille de tmp;k++) // on va recopier tmp dans T
T[k+p] = tmp[k] // tmp est la partie de T qui
commence à p
}
On peut aussi avoir des problèmes dû au langage. En effet, quand
le langage évalu la condition
(si b>r || (a<=r && T[a]<T[b]), il faut que si b>r la
seconde partie de la condition ne soit pas testée. En effet, on imagine
qu'il n'y a plus d'éléments dans b : donc, on les prend dans
a. Mais si le langage teste T[a]<T[b] il y aura un problème : b
peut sortir du tableau, donc ne plus exister et poser un problème d'accès
! Dans ces cas là, on sépare en plusieurs if/else les conditions
de test...
Un exemple de tri par fusion pour illustrer tout ceci :
Le tri par fusion a toujours la même complexité, il n'a pas
de meilleur ou de pire cas. La méthode qui permet de fusionner un tableau
de taille n est en (n) : quelques
comparaisons et ajouts d'indice, et surtout le parcours complet deux fois
du tableau (une fois pour le trier, une autre pour le recopier). Comme nous
sommes dans un algorithme récursif, on peut décrire sa complexité
par une relation de récurrence bien mathématique. Soit T(n)
le temps pour trier un tableau de taille n par le tri fusion, T(n) = 2T(n/2)
+ (n) avec le 2T(n/2) pour
la division du tableau et le (n)
pour la méthode de fusion.
Si on examine cette relation de récurrence sous la forme d'un arbre
binaire avec la division du tableau en deux, on s'aperçoit qu'on pourra
diviser ln(n) fois. Au final, nous sommes donc en (n.log(n)).
Pour résumer, l'algorithme de tri par fusion est en (n.log(n)),
ce qui est bien meilleur que les trois algorithmes de tris simples précédents
! Cependant, il y a un problème... En effet, le tri n'est pas fait
sur place : avec la méthode fusionner on voit qu'il y a la création
de tableaux supplémentaires (et dans un algorithme récursif,
on pense aussi à la remontée des résultats dans la pile...).
En bref, cela consomme de la mémoire en plus. Pour une application
sur un ordinateur personnel, ce n'est pas forcément dérangeant,
mais pour d'autres cas on doit limiter la consommation de mémoire :
exemple, dans un satellite les mémoires consomment de l'énergie,
et on préfère parfois attendre un peu plus longtemps plutôt
que de décharger le satellite...
Comme les précédents, on notera que c'est un tri stable.
9. Tri rapide (quick sort) >> vers le sommaire
On a vu que le tri précédent a une complexité intéressante mais que sa fusion consomme trop de mémoire. Une amélioration consiste donc à diviser le tableau en deux sous-tableaux [p, q] et [q+1, r] de façon telle que tous les éléments de [p, q] soient inférieurs aux éléments de [q+1, r]. Dans notre méthode "diviser, régner, réunir", on va donc gagner du temps pour ce qui est de "réunir".
Le gros problème consiste donc à bien faire cette division. Pour cela, le tri rapide choisit un élément qu'on nomme le pivot : il marque la séparation entre les deux tableaux. Donc tout élément inférieur au pivot ira à gauche et les autres éléments iront à droite.
La méthode récursive du tri rapide ressemble fortement
à celle du tri par fusion :
méthode Tri-Rapide(T un tableau, p et r des indices){
si p<r {
entier q = partitionner(T,p,r) //
le but est de choisir un bon pivot
Tri-Rapide(T,p,q-1) // Comme avant
on divise (mais plus forcément en moitié)
// le q est normalement déjà
à sa place. On ne le touche donc plus
Tri-Rapide(T,q+1,r) // On divise
donc en deux parties judicieusement choisies
// et là, plus besoin de
fusionner !
}
}
L'algorithme récursif reste simple, attaquons nous maintenant à
la méthode qui permet de partitionner. Ainsi :
méthode partitionner(T un tableau, p et r des indices){
soit x l'élément T[p] // on prend T[p] comme pivot
soit i = p // on définit i comme l'indice qui va monter, au départ
à p
soit j = r // on définit j comme l'indice qui va descendre, au départ
à r
tant que(vrai){ //On fait une boucle infinie. La condition de sortie sera
interne
pour(;i>r ou T[i]>x;i++) //Amene i à
la 1ère valeur > au pivot ou sort
pour(;T[j]<=x ou j==p;j--) //Amene
j à la 1ère valeur <= au pivot ou sort
si(i<=j){ // tant que les indices ne
se rencontrent pas ou ne se dépassent pas
element
tmp = T[i] // On permutte T[i] et T[j]
T[i] = T[j]
T[j] = tmp
}
sinon fin de boucle // dans un langage
comme Java ou C, on utilise "break"
}
// On va échanger l'indice qui descend avec notre pivot
element tmp = T[j]
T[j] = T[p]
T[p] = tmp
retourner j;
}
Une remarque : il y a plusieurs manières de coder cette méthode "partition" ; celle présentée ici n'est peut-être pas la plus simple, mais elle a au moins l'avantage d'être explicite et de fonctionner correctement. On touve plusieurs versions de cette méthode qui ne vérifient pas l'indice et sortent sans problème du tableau !
Utilisons l'ensemble pour trier le tableau 63, 66, 13, 25, 65, 20, 56, 99
:
Cet algorithme a corrigé le défaut de son prédecesseur
: c'est maintenant un tri sur place. Par contre, il n'est plus stable. Dans
le cas favorable où le partitionnement est équilibré
(tableaux de taille n/2 et (n/2)-1 à chaque appel), sa complexité
s'analyse avec la même relation de récurrence que le tri par
fusion, nous en tirons donc un (n.log(n)).
Par contre, dans le pire des cas où on a un partitionnement complétement
déséquilibré (tableaux de taille quasi nulle et n-1 à
chaque appel), la relation de récurrence devient T(n) = T(n-1) + n
- 1. Etant donné l'expression de cette récurrence, on voit immédiatement
qu'elle est égale à la somme des i - 1 pour i de 1 à
n ; on utilise la formule classique dans ce cas pour obtenir n(n-1)/2, donc
une complexité en (n²).
Ainsi, dans le pire des cas, le Tri-Rapide est en (n²),
ce qui est très mauvais ! Quand survient cette situation ? Lorsque
le tableau est déjà trié (dans un sens ou dans l'autre),
configuration où le tri à bulle ne mettait que (n)...
En bref, on s'aperçoit qu'il est très délicat de choisir
un bon algorithme de tri : les tris à bulles/insertion/sélection
sont globalement lent, le tri par fusion est très rapide mais consomme
de la mémoire, le tri-rapide consomme moins de mémoire mais
est lent si le tableau est déjà trié.
Les tris sont importants et nombreux, voici donc quelques ouvrages
:
- "Algorithmes en Java" de Robert Sedgewick. Un grand classique,
avec de nombreux exercices.
- "The art of computer programming (Volume 3)" de Donald Knuth.
La référence incontestable sur le sujet !
- "Introduction à l'algorithmique" de Cormen, Leiserson,
Rivest et Stein. Un classique pour démarrer.