Accueil > Dossiers > Algorithmique : Arbres binaires (2)

---

1. Introduction aux Arbres Binaires de Recherche (ABR) >> vers le sommaire

Dans le tutorial précédent, nous avions laissé de côté la question de l'organisation de l'arbre, en particulier des méthodes d'ajout et de suppression. Nous pouvons maintenant présenter l'organisation la plus classique, celle de l'Arbre Binaire de Recherche : pour chaque noeud n donné, tous les éléments du sous-arbre gauche ont une clé (l'information contenu dans le noeud) inférieure à n, et tous les éléments du sous-arbre droit une clé supérieure ou égale à n.

Les noeuds sont donc automatiquement classés selon l'information qu'ils contiennent. Cependant, il faut définir avec plus de précision la relation d'ordre "inférieure" et "supérieure ou égale". En effet, un noeud peut contenir n'importe quel type d'objet : un nombre, une chaine de caractère, une image, un son.. Explicitons donc l'opération de comparaison entre les différents éléments contenus dans les noeuds. Quelques exemples :
- Un nombre. Relation d'ordre immédiate : soient deux nombres a et b, on peut directement faire a<b et a>=b.
- Une chaîne de caractère. Relation d'ordre possible : comparer la taille de la chaîne. Ainsi, "table" est inférieur à "tableau", et "maison" est supérieur ou égal à "sac". On peut aussi définir un classement alphabétique : "table" est inférieur à "tableau" et "maison" devient inférieur à "sac".
- Un son. Relation d'ordre possible : la hauteur moyenne du son. Exemple : la voix d'un ténor est inférieure à celle d'une soprano.
- Une image. Relation d'ordre possible : le nombre de couleurs utilisées dans l'image, ou la taille sur le disque dur occupée par l'image...

Deux exemples :

Dans notre exemple en Java, nous définissons donc une nouvelle classe qui représentera les objets contenus dans les noeuds, et implémentera l'opération de comparaison :

 

2. Recherche du maximum et du minimum dans un ABR >> vers le sommaire

Cette recherche est très simple. On sait que pour un noeud n donné, tous les éléments du sous-arbre gauche ont une clé inférieure, ou tous ceux du sous-arbre droit une clé supérieure ou égale. Comme on peut le voir sur les exemples d'arbres précédents, on obtient le plus petit élément en partant de la racine et en prenant le fils gauche ; de même, on obtient le plus grand élément en partant de la racine et en prenant le fils droit. D'où le code :

Dans le pire des cas, le noeud que l'on cherche est le plus éloigné de la racine ; ce sera donc lui qui donnera la hauteur de l'arbre. Autrement dit, dans le pire des cas cette recherche est en O(n*log(n)), qui est la hauteur de l'arbre. Par contre, dans le meilleur des cas, le noeud que l'on cherche est directement à côté de la racine, il n'y a donc qu'une opération à faire : O(1).

 

3. Recherche d'un contenu quelconque dans un ABR >> vers le sommaire

Les règles de l'ABR nous permettent de ne pas avoir à regarder chaque noeud pour savoir s'il contient l'information recherchée. On compare en effet au noeud courant : si l'information qu'on cherche est inférieure, on va chercher dans le sous-arbre gauche ; si elle est supérieure, on cherche dans le sous-arbre droit. On utilise les opérateurs de comparaison définis dans la classe Contenu, et on code ainsi :

 

4. Ajout dans un ABR >> vers le sommaire

Pour conserver les propriétés de notre ABR, il va falloir effectuer une série de tests sur le noeud à ajouter afin de le placer au bon endroit. On aura besoin d'informations complémentaires sur le noeud, par exemple son parent. Ainsi, on complète la classe Node :

Regardons maintenant la situation lorsqu'on ajoute un noeud n :
si la racine de l'arbre est vide, alors la racine devient ce noeud
sinon //ceci est notre boucle de traitement
      soit r la racine
      si n < r
              si le fils gauche de r est vide, alors fils gauche de r = n
              sinon, recommencer la boucle de traitement en considérant r comme fils gauche de r
      sinon
              si le fils droit de r est vide, alors fils droit de r = n
              sinon, recommencer la boucle de traitement en considérant r comme fils droit de r

Ceci se traduit facilement en Java :

 

5. Suppression dans un ABR >> vers le sommaire

La suppression risque de modifier la structure de l'ABR, et il y a donc plusieurs changements à effectuer ; c'est une méthode plus complexe à coder. Pour cela, nous devons introduire la notion de successeur : soit un noeud n, alors le noeud ayant une clé immédiatement supérieure à n est son successeur. Un exemple :

On trouve le successeur d'un noeud de la façon suivante :
soit n un noeud dont on veut le successeur
si n a un sous-arbre droit   // on va dans les clés qui sont les plus grandes...
     alors le successeur de n est le minimum de ce sous-arbre   // et on prend la plus petite
sinon  // on doit remonter dans l'arbre
     soit x le parent de n
     // principe : si on est fils droit, alors notre père est plus petit, on doit encore remonter
     // sinon (c'est-à-dire si on est fils gauche) alors notre père est plus grand, c'est ok
     tant que n est le fils droit de x et que x n'est pas nul
          n devient x //on remonte encore
          x devient le parent de x
// si on arrive ici, x est le parent dont la clé est immédiatement supérieure
le successeur de n est x

Une fois encore, la traduction de ce code est immédiate :

On peut maintenant distinguer les trois cas de suppression :
- Le noeud qu'on supprime n'a pas de fils. Il ne dérange donc rien, aucun problème.
- Le noeud qu'on supprime a un seul fils. On peut alors remplacer ce noeud par son fils directement.
- Le noeud qu'on supprime a 2 fils. Là, c'est délicat. On remplace le noeud à supprimer par son successeur (c'est-à-dire le noeud de contenu immédiatement supérieur), et on supprime le successeur.

Le code est plus compliqué :

6. Caractéristique complémentaire d'un arbre : la hauteur >> vers le sommaire

Nous avions vu le terme de hauteur dans le tutorial précédent. La hauteur issue d'un noeud est la distance qui sépare ce noeud du plus lointain de ses fils. Ainsi :

 

7. Introduction aux arbres équilibrés : les rotations >> vers le sommaire

Il existe des spécifications de l'ABR que nous avons vu qui fixent une hauteur maximale ou d'autres paramètres. Pour répondre à ces paramètres, il existe des opérations qui vont redonner son équilibre à l'arbre : il s'agit des rotations (droite ou gauche).

On se donne un noeud et on choisit de faire une rotation droite ou gauche. Dans l'exemple ci-dessous, on fait une rotation droite sur le noeud A, ou une rotation gauche sur le noeud B :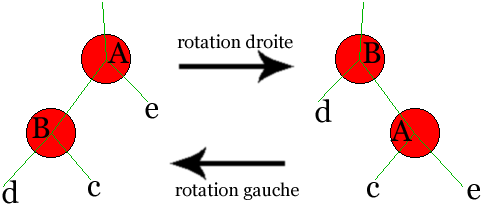

Sur notre graphique avec A, B, c, d et e, tentons de décrire le processus de rotation droite sur A :
soit B le fils gauche de A
le fils gauche de B devient le fils droit de A
le parent de B devient le parent de A
le fils droit de B devient A

Il y a beaucoup de choses implicites qu'on voit apparaître dans le code. Notamment un principe simple : soient deux noeuds x et y ; si x devient fils de y, alors il faut penser à faire la mise à jour dans x (pour le père) et dans y (dans le fils droit ou le fils gauche). On a donc le code suivant pour la rotation droite et la rotation gauche :

Faisons quelques exemples :

 

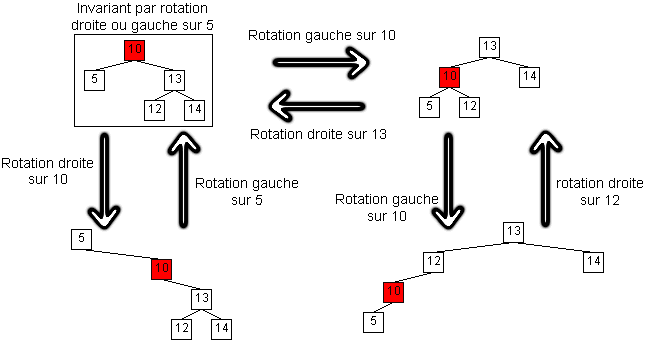
8. Les arbres rouge-noir (ARN) >> vers le sommaire

Afin d'optimiser les ABR, on a étendu leurs propriétés de deux façons ; les arbres rouge-noir, ou ARN sont l'une d'entre elle. Les noeuds ont deux couleur : rouge, ou noir ; ceci respectant les règles suivantes en plus de celles des ABR :
- La racine est noire
- Les feuilles sont noires
- Si un noeud est rouge, ses deux enfants sont noirs
- Pour tout noeud de l'arbre, les chemins de ce noeud vers les feuilles qui en dépendent ont le même nombre de noeuds noirs

On peut donner deux exemples :

Dans un ARN, un noeud a une caractéristique supplémentaire : sa couleur. On peut donc mettre au point une classe ColorNode adaptée à l'ARN :

Du point de vue de notre implémentation en Java, on tire parti des bénéfices du langage objet en définissant un ARN comme une extension d'un ABR. Ceci voulant dire qu'on prend toutes les méthodes définies dans la classe 'Arbre', et qu'on peut rajouter ou redéfinir celles qui nous intéresses. Dans certains cas, on peut éviter de réécrire de grosses portions de code. Ici, nous sommes plus restreint par un problème : dans un ARN nous utilisons un ColorNode tandis que dans un ABR nous avons un Node. Nous importerons donc toutes les méthodes qui ne font pas référence au type de noeud mais devrons redéfinir ou éviter d'utiliser les autres. Ainsi :

Dans un ARN comme dans un ABR, la configuration de l'arbre peut-être changée par les méthodes ajout/suppression. La situation est pire dans un ARN puisque la méthode d'ajout peut entrainer une série de modifications à faire : en effet, il y a un trajet à respecter ("pour tout noeud de l'arbre, les chemins de ce noeud vers les feuilles qui en dépendent ont le même nombre de noeuds noirs"). Pour résoudre ceci, on implémente les méthodes de rotation gauche et de rotation droite dans l'ARN.

Le principe est le suivant :
on veut insérer une information dans notre arbre
si la racine est vide, alors on met l'information dans la racine
sinon
      on appelle la fonction qui va se charger de l'ajout complet
           celle-ci place le noeud dans l'arbre (comme dans un ABR) puis équilibre l'arbre

Ceci est donc effectué par les méthodes du code suivant :

---

Le pack java Arbres.zip contient tout ce qui a été fait dans ce tutorial et le précédent, avec en plus la possibilité de visualiser les arbres et donc de les tester (classe Afficheur).

Quelques conseils et propositions d'exercices :
- Construire pas-à-pas l'algorithme de suppression dans un ABR
- Construire pas-à-pas l'algorithme d'ajout dans un ARN (la partie qui équilibre)
- Trouver l'algorithme de suppression dans un ARN
- Chercher les principes des arbres AVL
- Du point de vue code en Java, agrandir la classe Arbre et créer la classe ABR et ARN comme des extensions de cette classe de façon telle qu'on ne trouve dans l'ABR et l'ARN que les méthodes d'ajout et de suppression (avec au besoin un Main pour tester)