




1. Rechercher un élément dans une liste >> vers le sommaire
Dans une liste donnée, on souhaite rechercher un élément.
Sachant que la liste n'a aucun ordre, l'élément recherché
peut-être n'importe où, voire même ne pas se trouver dans
la liste. Ainsi, pour le rechercher, on doit parcourir tous les éléments
un par un ; soit, dans le cas d'une simple ArrayList :

Dans le pire des cas, l'objet recherché ne se trouve pas dans la liste. Soit n le nombre d'objets dans la liste, l'opération de recherche se fait donc dans le pire des cas en O(n).
On souhaiterait disposer d'une structure de données principalement axée sur la recherche, et qui ait donc une complexité plus faible pour cette opération. Pour cela, on introduit les arbres (dont on montrera dans le tutorial suivant les propriétés qui permettent une recherche optimale).
2. Définition d'un arbre >> vers le sommaire
Un arbre est un ensemble de noeuds (les ronds rouges) reliés
par des arêtes (les traits verts), de façon telle qu'il existe
un chemin unique entre deux noeuds. Le vocabulaire employé relève
de la généalogie et de la botanique :
- on considère l'arbre comme étant constitué de différents
niveaux (selon les définitions, commencant à 0 ou 1)
- le noeud du premier niveau est nommé la Racine
- si des noeuds sont reliés à un noeud x de niveau inférieur,
alors ils s'appellent les fils de x. Autrement dit, x est leur père
- un noeud sans fils est une feuille

On peut aussi définir des ensembles de noeuds et d'arêtes
de l'arbre :
- On nomme 'branche' un chemin de la racine à une feuille. La plus
longue branche existante donne la hauteur de l'arbre.
- On peut extraire d'un arbre un sous-arbre, en prenant n'importe quel noeud
et ce qui en découle.
Si un arbre est tel que chaque noeud a au plus N fils, l'arbre est dit n-aire. Nous allons étudier les arbres 2-aire (dits 'binaires'), c'est-à-dire ayant au plus 2 fils par noeud.

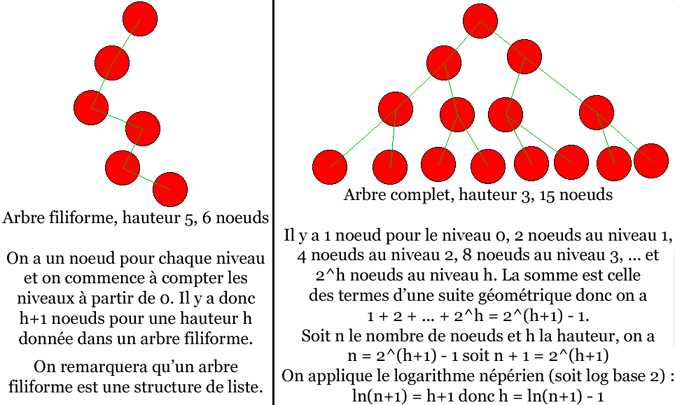
On peut introduire deux arbres binaires bien particuliers :
- l'arbre filiforme, où tout noeud n'a au maximum qu'un fils
- l'arbre complet, où tous les niveaux sont remplis au maximum
3. Utilisation d'un tableau pour représenter un arbre binaire >> vers le sommaire
On remarque que dans un arbre binaire, le noeud numéro
i a comme fils gauche le noeud 2i et comme fils droit le noeud 2i+1 :

Ainsi, on peut stocker l'ensemble dans un tableau : on a un
noeud d'indice i, son fils gauche est un noeud d'indice 2i et son fils droit
un noeud d'indice 2i+1. Voyons donc un arbre binaire et le tableau permettant
de le stocker :

Cette façon de faire a les avantages et les inconvénients
typiques d'une structure de tableau :
- accès en temps constant à n'importe quel élément
- le tableau peut-être plein, il faut l'agrandir, ce qui est une opération
coûteuse
- il peut y avoir des cases vides, donc une occupation mémoire abusive
On préfèrera donc utiliser une implémentation par chaînage, avec l'objet Noeud que l'on a vu précédemment.
4. Utilisation de noeuds >> vers le sommaire
L'objet noeud de notre arbre binaire contient une information,
un lien vers son fils droit et un lien vers son fils gauche. Le code est donc
évident :

Il existe de nombreux arbres binaires différents, selon
la façon dont on les organise. Cette façon se retrouve surtout
dans les opérations 'ajouter' et 'supprimer' ; en effet, on doit mettre
le nouveau noeud de façon à ce qu'il respecte la structure établie
(pour essayer de répartir au mieux les informations), et retirer un
noeud de façon à ce que la structure soit conservée.
Le canevas d'un Arbre, en ignorant le code de ces deux méthodes, est
donc :
5. Parcourir l'arbre: préfixé, infixé, postfixé >> vers le sommaire
Parcourir l'arbre consiste à suivre les connexions entre
les noeuds, sans exploiter l'information qu'elles renferment. Le parcours
est donc dépendant de la structure de l'arbre (exemple : binaire, 5-aire...)
mais pas du modèle d'organisation des données. Les trois parcours
de base sont les suivants :
- Préfixé : racine, sous-arbre gauche, sous-arbre droit
- Infixé : sous-arbre gauche, racine, sous-arbre droit
- Postfixé : sous-arbre gauche, sous-arbre droit, racine
Les arbres ayant une structure fortement récursive, les
algorithmes le sont aussi. Voici donc les parcours :

Pour mieux comprendre, quelques exemples de ces parcours :

Le principe de ces parcours est de lire le contenu des noeuds dans un certain ordre et d'exécuter parfois des opérations. Le second arbre nous permet par exemple de stocker un calcul ; c'est une structure souvent utilisée. Il est donc courant d'avoir aussi à sa disposition les méthodes permettant d'évaluer une expression, par exemple en postfixé (le plus simple).
En examinant la façon dont est contruite une expression en postfixé,
on a une idée du raisonnement :
soit p une pile
on parcours l'expression
si on lit une opérande, on l'empile
sinon si on lit un opérateur
on
depile, on depile, on effectue l'opération, et on empile le résultat
sinon on affiche un message d'erreur
renvoyer le résultat
Faisons tourner ceci sur l'expression 1 2 * 3 4 + * :
on lit 1 : c'est une opérande, on l'empile (état de p : [1])
on lit 2 : c'est une opérande, on l'empile (état de p : [2])
on lit * : c'est un opérateur, on depile (2), on depile (1), on effectue
1*2 = 2, on empile le résultat (p : [2])
on lit 3 : c'est une opérande, on l'empile (état de p : [2][3])
on lit 4 : c'est une opérande, on l'empile (état de p : [2][3][4])
on lit + : c'est un opérateur, on depile (4), on depile (3), on effectue
3+4 = 7, on empile le résultat (p : [2][7])
on lit * : c'est un opérateur, on depile (7), on depile (2), on effectue
2*7 = 14, on empile le résultat (p : [14])
on a fini de lire, et la pile contient uniquement un résultat
le résultat est 14
On peut proposer une implémentation en Java pour évaluer une
expression en postfixé :

De même, on peut construire le raisonnement pour évaluer une
expression en préfixé, un peu plus complexe :
soit p une pile
on parcours l'expression (implicite : de gauche à droite, classiquement)
si on lit un opérateur, on l'empile
sinon si on lit une opérande (c'est-à-dire
un chiffre...)
si
le dernier élément de la pile est une opérande
alors
depiler p pour avoir l'opérande, depiler p pour avoir l'opérateur,
faire l'opération
puis
stocker le résultat dans la pile
sinon
on l'empile
sinon on affiche un message d'erreur
renouveler le traitement en lisant le contenu de la pile jusqu'à ce
qu'elle contienne juste le résultat
Faisons tourner ceci sur l'expression * * 1 2 + 3 4 :
on lit * : c'est un opérateur, on empile (état de p : [*])
on lit * : c'est un opérateur, on empile (état de p : [*][*])
on lit 1 : c'est une opérande, le dernier élément de
p n'est pas une opérande, on empile (état de p : [*][*][1])
on lit 2 : c'est une opérande, le dernier élément de
p est une opérande, on depile (1), on depile (*), on
fait
l'opération 1 * 2 = 2, et on empile (état de p : [*][2])
on lit + : c'est un opérateur, on empile (état de p : [*][2][+])
on lit 3 : c'est une opérande, le dernier élément de
p n'est pas une opérande, on empile (p : [*][2][+][3])
on lit 4 : c'est une opérande, le dernier élément de
p est une opérande, on depile (3), on depile (+), on fait
l'opération
3 + 4 = 7, on empile (p : [*][2][7])
on a fini de lire, et la pile ne contient pas uniquement un résultat
on lit l'expression * 2 7 dans la pile, on reprend le traitement en transmettant
l'expression dans la pile :
on lit * : c'est un opérateur, on empile (état de p : [*], notons
que c'est bien une nouvelle pile)
on lit 2 : c'est une opérande, le dernier élément de
p n'est pas une opérande, on empile (état de p : [*][2])
on lit 7 : c'est une opérande, le dernier élément de
p est une opérande, on depile (2), depile (*), on fait
l'opération
2 * 7 = 14, on empile (p : [14])
on a fini de lire, et la pile contient uniquement un résultat
le résultat est 14
D'où l'implémenation en Java permettant d'évaluer une
expression en préfixé, s'appuyant sur les méthodes utilisées
dans l'évaluation précédente (en postfixé) :

Ceci doit surtout vous donner une idée du raisonnement et l'utilisation importante de la pile dans la lecture de ces expressions. Après, on introduit des notions plus complexes : priorité des opérateurs (donc des positions différentes dans l'arbre), gestion des erreurs (exemple d'un arbre avec un père *, un fils 1, et un autre fils à 'null')... Pour passer d'une expression d'un type dans une autre, on utilisera aussi une pile.
6. Parcourir l'arbre : en hauteur ou en largeur >> vers le sommaire
Il existe deux autres parcours d'arbre, qui consistent à se propager de haut en bas (de la racine vers les feuilles) ou de gauche vers droite (commencer à la racine, puis parcourir chaque niveau en largeur).
Pour le parcours en hauteur, il ne s'agit en fait que d'un des trois parcours
(infixé, préfixé, postfixé) étudiés
précédemment. On y adjoint simplement un lanceur si on veut
explorer la totalité de l'arbre :

Le parcours en largeur est identique au parcours en hauteur utilisant une
pile, mais on va prendre cette fois-ci une file :

Vous pouvez télécharger les fichiers en Java dont sont isssues les captures d'écrans de code (à l'exception de la recherche dans un tableau, bien évidemment) : Arbre.zip
Les arbres sont une structure fondamentale que nous allons continuer à
étudier dans le tutorial suivant. Aussi, il est recommandé de
bien maîtriser cette base. Ainsi, quelques conseils :
- faire tourner les algorithmes de parcours en largeur et en hauteur
- trouver l'algorithme pour calculer une expression en infixé
- trouver des algorithmes permettant de passer d'une expression postfixé
à une préfixé, infixé à postfixé,
etc.
- faire une implémentation d'un arbre en utilisant un tableau